El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de los catetos (los dos lados menores del triángulo, los que conforman el ángulo recto).
1.3.1 Demostración gráfica
Nueva entrega de nuestra sección dedicada a mostrar applets de ese gran programa de geometría llamado GeoGebra. En esta ocasión se trata de un applet de nuestro amigoIgnacio Larrosa, que podéis encontrar aquí, en el que se nos muestra una demostración visual del teorema de Pitágoras. Ahí va:
http://gaussianos.com/lo-que-se-puede-hacer-con-geogebra-ix-demostracion-visual-del- teorema-de-pitagoras/
1.3.2 El teorema en 3D
1.4 Teorema de Tales
Dos triángulos son semejantes cuando tienen sus ángulos homólogos iguales y sus lados homólogos proporcionales.
A=A' B=B' C=C'
1.4.1 Primera teorema
Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado.
Corolario
Del establecimiento de la existencia de una relación de semejanza entre ambos triángulos se deduce la necesaria proporcionalidad entre sus lados. Ello significa que la razón entre la longitud de dos de ellos en un triángulo se mantiene constante en el otro.
Por ejemplo, en la figura se observan dos triángulos que, en virtud del teorema de Tales, son semejantes. Entonces, del mismo se deduce a modo de corolario que el cociente entre los lados A y B del triángulo pequeño es el mismo que el cociente entre los lados D y C en el triángulo grande. Esto es, que como por el teorema de Tales ambos triángulos son semejantes, se cumple que:
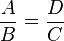
- 1.4.2 Segunda teorema
- Sea B un punto de la circunferencia de diámetro AC, distinto de A y de C. Entonces el triángulo ABC, es un triángulo rectángulo.




No comments:
Post a Comment