2.1 ¿Que es un lugar geométrico?
-Un lugar geométrico es un conjunto de puntos que satisfacen determinadas propiedades geométricas.
2.2 La mediatriz y la bisectriz
-La mediatriz
Es la línea recta perpendicular a dicho segmento trazada por su punto medio. Equivalentemente se puede definir como el lugar geométrico — la recta — cuyos puntos son equidistantes a los extremos del segmento. También se le llama simetral.
-La bisectriz
Es la recta que pasa por el vértice del ángulo y lo divide en dos partes iguales. Es el lugar geométrico de los puntos del plano que equidistan (están a la misma distancia) de las semirrectas de un ángulo.
2.3 Las cónicas
Se denomina sección cónica (o simplemente cónica) a todas las curvas intersección entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen las cónicas propiamente dichas. Se clasifican en tres tipos: elipse,parábola e hipérbola. un cono circular recto de dos hojas con un plano que no pasa por su vértice
De acuerdo al ángulo y el lugar de la intersección es posible obtener círculos, hipérbolas , elipses o parábolas. Cuando el plano solo toca uno de los mantos del cono y no es paralelo a una de sus aristas se obtiene una Elipse. Cuando el plano corta los dos mantos del cono se obtiene una hipérbola. Cuando el plano que corta es paralelo a una de las aristas del cono se obtiene una parábola.
Tipos:
En función de la relación existente entre el ángulo de conicidad (α) y la inclinación del plano respecto del eje del cono (β), pueden obtenerse diferentes secciones cónicas, a saber:
- β < α : Hipérbola (naranja)
- β = α : Parábola (azulado)
- β > α : Elipse (verde)
- β = 90º: Circunferencia (un caso particular de elipse) (rojo)
Si el plano pasa por el vértice del cono, se puede comprobar que:
- Cuando β > α la intersección es un único punto (el vértice).
- Cuando β = α la intersección es una recta generatriz del cono (el plano será tangente al cono).
- Cuando β < α la intersección vendrá dada por dos rectas que se cortan en el vértice.
- cuando β = 90º El ángulo formado por las rectas irá aumentando a medida β disminuye, hasta alcanzar el máximo (α) cuando el plano contenga al eje del cono (β = 0).
2.3.1 La circunferencia
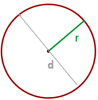
La circunferencia es una curva plana y cerrada donde todos sus puntos están a igual distancia del centro. Resultado de la observación plurimilenaria de las circunferencias concéntricas al arrojar una piedra sobre un espejo de agua o el borde de una fruta- naranja, limón, guayaba, etc- cortada perpendicularmente a su eje de suspensión.Una circunferencia es el lugar geométrico de los puntos de un plano que equidistan de otro punto fijo y coplanario llamado centro en una cantidad constante llamada radio.
Tipos:
-Cuerda
La cuerda es un segmento que une dos puntos de la circunferencia.
-Diámetro
El diámetro es una cuerda que pasa por el centro de la circunferencia.
El diámetro mide el doble del radio.
-Arco
Un arco es cada una de las partes en que una cuerda divide a la circunferencia.Se suele asociar a cada cuerda el menor arco que delimita.
-Semicircunferencia
Una semicircunferencia es cada uno de los arcos iguales que abarca un diámetro.
Longitud de una circunferencia
La longitud de una circunferencia es igual a pi por el diámetro.
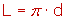
La longitud de una circunferencia es igual a 2 pi por el radio.












No comments:
Post a Comment